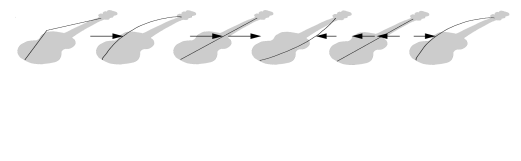
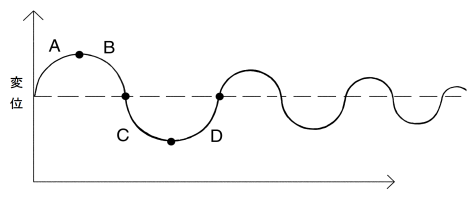
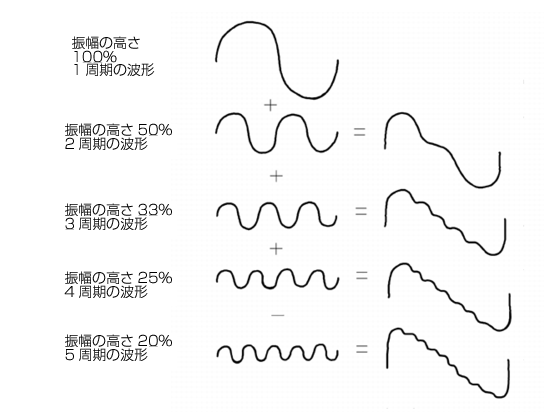
SONAR LE Documentation is based on the full version of SONAR. Some screenshots, folder paths, features and other references may differ from your installation.

ギターの弦の場合

音の発生プロセスをもっと良く理解するために、ギターの弦についてみてみましょう。

指でギターの弦をはじく時、弦の全体がある一定の率で前後に動き始めます。弦が一秒間に前後に動いた回数を周波数とよびます。周波数はHz（ヘルツ）という単位を用いてあらわされます。音の周波数は非常に高いため、kHz（キロヘルツ：ヘルツの1000倍）で表されることもあります。

実際に弦が動く幅のことを、振幅と呼びます。この幅は、どれほど激しく弦がはじかれるかに比例します。振幅が大きいほど、強い音になります。

弦の振幅は、以下のように、弦が振動するにつれて変化します。

ピックによってはじかれた弦は、元の位置に向かって戻り始めると、元の位置を通過してそのまま反対側の限界まで動きます、さらに元の位置に向かって再び戻っていきます。このパターンは、空中分子の摩擦によって熱に変換され尽くすまで、連続して繰り返されます。弦が振動すると、周りの空気分子も同様に振動します。振動は音波として空気中を伝搬します。その振動が耳に入ると、それによって鼓膜が振動します。これによって音が聞こえるのです。同様に、振動している空気がマイクロホンに当たったら、マイクロホンが振動して、そして電気の信号が送られます。

人間が音として聴こえるためには、振動の周波数は少なくとも20Hz以上でなければなりません。人間が聞くことができる最も高い周波数は、理論的には20kHzですが、実際は、15あるいは17kHzあたりでしょう。他の動物やマイクロホンは、音として聞くことのできる範囲が異なります。

弦の単純な前後の動きが、音を作り出す唯一の動きなのであれば、すべての弦楽器は恐らくほぼ同じ音に聞こえるでしょう。しかしながら、実際にはそうではありません。物理学の法則はそれほど単純ではないのです。実際、弦はその全部の長さの振動だけではなく、2分の1の長さ、3分の1、4分の1、5分の1といった長さでも振動します。これらの付加的な振動（倍音）は、もともとの振動（基本音）より速いですが、通常、強さにおいては弱くなります。しかしながら、私達の耳は、個々の倍音を1つ1つ聞くわけではありません。もしそうだとしたら、1本の弦で演奏された時でも、常に和音に聞こえるはずです。実際にはそうではなく、すべての振動は、複雑に複合されて音を形成し、私達の耳には1つの音色として聞こえます。

この複合された音の波形は、まだそれぞれの楽器の音の個性を表現していません。たとえば、通常弦楽器には共鳴器があります。ギターの場合、共鳴器は中が空洞になった木で、そこに弦が取り付けられています。つまりこれがギターのボディです。ギターのボディは、ギターが演奏された時に聴こえる音の印象に大きなインパクトを与えます。なぜなら、ボディが、弦による振動を強めたり、弱めたりするからです。同時に起こっているすべての振動の効果が、共鳴器によって変更されて、我々がギターとして知っている響きになるのです。

 

関連項目：

デジタルオーディオの基礎知識